2020.11.10笔记
2020.11.10笔记
SAO
树形图拓扑序计数。
有两个做法,直接 $DP$ 和 容斥。
容斥的做法下一道题会讲,因为下一题只能容斥。
是树形图姑且就先当成树来考虑
设 $f_{i, j}$ 表示以 $i$ 为根的子树中,$i$ 的排名为 $j$ 的方案数。
转移考虑合并子树,即合并以 $u$ 为根的已处理的子树,和 $u$ 的儿子 $v$ 的子树。
相当于合并两个序列 $q_1, q_2$,合并之后两个序列内部依然有序。
考虑 $v$ 在 $u$ 之前的情况:
枚举一个 $k$,表示 $v$ 这个子树的序列前 $k$ 个都在 $i$之前。
$$f_{u, i+j} = \sum_{k=j}^{sz_v}\binom{i+j-1}{i-1}\binom{sz_u+sz_v-i-j}{sz_u-i}f_{u, i} \times f_{v, j}$$
显然可以前缀和优化掉枚举 $k$,可以做到 $O(1)$ 转移。
另一种情况是类似的,不讲了。
【CTSC2019】氪金手游
先来考虑一个子树中根节点最先出现的概率怎么计算。
设 $sum_u$ 表示以 $u$ 为根的子树中 $w_i$ 的和,设 $n$ 个点的总和为 $tot$。那么也就是说子树内都不能先出现,可以出现子树外的。
那么概率为:
$$\frac{w_u}{tot}\sum_{i=0}^{\infty}{(\frac{tot-sum_u}{tot})^i}=\frac{w_u}{sum_u}$$
现在如果是外向树的话,可以轻松计算合法的方案的概率了,但是有反向边,考虑容斥。
合法的方案是满足所有边的限制,那么不合法的方案就是违反某些限制,体现在反向边上就是当做正向边来处理。总方案数是不考虑限制随便安排顺序,那么相当于这条边不存在,可以看做是一个独立的子树。
可以设 $f_{u, i}$ 表示以 $u$ 为根的子树,$w$和为 $i$时,合法的概率。
转移的时候可以当做树形背包转移。
- 如果是正向边则直接转移。
- 如果是反向边变成正向边要带上容斥系数;忽略的话要当做这个子树不存在,不能统计 $w_i$ 的和。
CSP.AC 296
对于 $m$ 较小的情况,线段树直接维护矩阵乘法即可。
但是 $m$ 较大的话会出问题。
但是可以注意到修改极少,只有 $10^5$,因此可以将修改离线,然后离散化。
可以发现很多段都始终不被修改,而且都是空白的,这些地方可以矩阵快速幂求出。
而修改的位置暴力改即可。
csp.ac 297
经典题了,多了个已经建好的泉水。
那么选择这个泉水的位置为根可以避免根是个叶子。
然后套用经典的贪心做法:
每次拿出最深的叶子,尽可能往上跳 $k$ 步,然后放下泉水,修改掉没被覆盖的叶子,复杂度为 $n^2$ 。
csp.ac298
前八十分直接求 $LIS$ 即可。
后面的二十分一开始以为可以按照第一维排序之后二维树状数组,但是写完交上去发现不对劲。
原因大概是没有考虑到所有的情况。
其实不需要动用数据结构强行多两个 $\log$。
可以暴力将图建出来直接求最长路,复杂度是 $O(n^2)$ 的。
csp.ac299
非常有意思的题。
可以发现 $a_i$ 每隔两个位置必定乘以 $2$,因此五十几项之后就会超过 $10^9$。
超过范围之后,新产生一个奇数位置必然毫无用处,产生的偶数位会贡献 $mex$,因此可以暴力预处理出前五十几项的答案。
- 对于一次询问,若在前面出现过,那么直接输出即可;
- 否则一定是通过偶数位的 $mex$ 产生的,可以计算需要多少项。
csp.ac300
看起来就像是一道贪心题,但是反复尝试某些贪心策略都可以发现是错的。
首先很显然的一件事情是,对于某个询问,必然是按照 $a_i$ 不降的顺序依次吃。
大胆猜想,可以增量构造依次构造每个询问要吃的菜的集合(请注意后加入的菜未必后吃)。
按照起点排序之后,依次考虑进行贪心。
记当前的时间为 $t$,目前可以吃的菜中时间最短的为 $now$,下一个没考虑的菜编号为 $i$。
- 若 $t+now \leq a_i$,那么直接吃 $now$即可;
- 否则要考虑进行一些调整,先空吃掉 $a_i-t$ 这段时间,再将 $now$ 修改为 $now-(a_i-t)$,再扔进堆里。
第二种情况的正确性在于,会出现新加入集合的某道菜在询问小的时候先吃,而以后后吃;假装空吃掉一段之后可以对齐菜的起点从而正确调整答案。
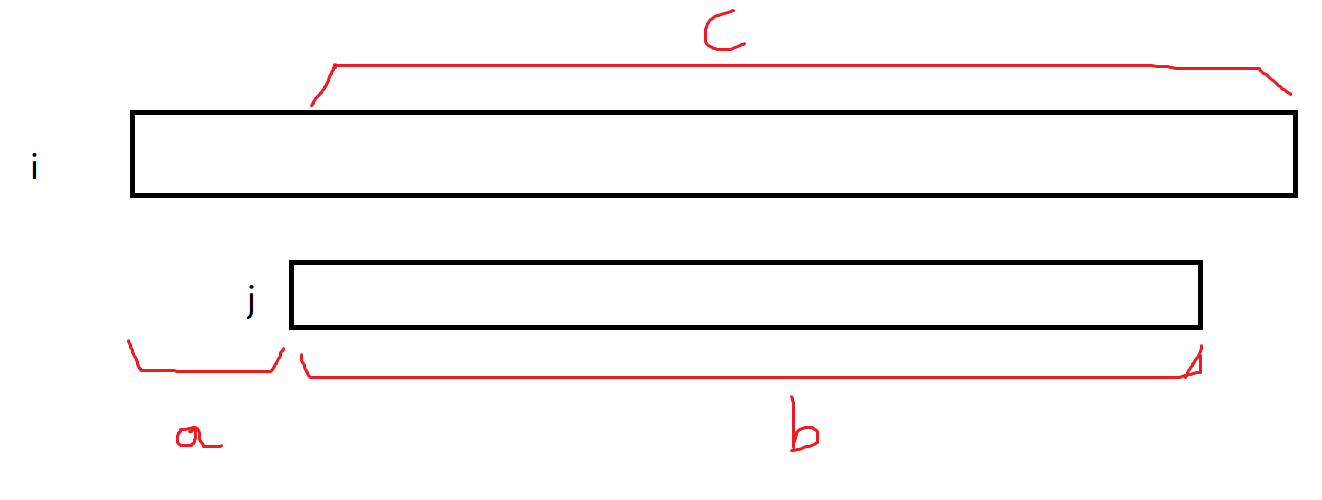
下面是一个例子:
需要吃一盘菜的时候,应该选择先吃 $j$;
需要吃两盘菜的时候,应该是先吃 $i$ 再吃 $j$。
对应到做法中所提到的就是先吃 $a$ 这个空白段,然后再吃 $b$ 这一段,再吃 $c$ 这一段。